Repeated Prisoner's Dilemma
Abstract
This project explores the Repeated Prisoner's Dilemma, a fundamental concept in game theory with significant real-world applications. By implementing and analyzing various strategies based on Robert Axelrod's groundbreaking work, we investigate which approaches perform best in long-term competitive scenarios. The project includes a comprehensive tournament between 20+ different strategies, providing insights into cooperation, defection, and strategic decision-making. The results demonstrate that successful strategies typically follow the principle: "Be nice, be forgiving, but don't be a pushover." This research has applications in business competition, international relations, and social behavior analysis.
Introduction
The Prisoner's Dilemma is a classic game theory experiment with significant real-world applications. It involves two parties who must decide independently whether to cooperate or defect, with the following outcomes:
- If both cooperate, both receive a moderate reward
- If one defects while the other cooperates, the defector receives a large reward while the cooperator gets nothing
- If both defect, both receive a minimal reward
In the Repeated Prisoner's Dilemma, this game is played multiple times, allowing players to adjust their strategies based on previous outcomes. This repetition introduces the possibility of strategies that consider the history of interactions, leading to more complex and nuanced decision-making.
Real-World Applications
The Repeated Prisoner's Dilemma models many real-world situations where individuals or groups interact repeatedly over time. Understanding these dynamics is crucial for analyzing:
- Business Competition: Companies deciding between competing aggressively or cooperating through practices like price-fixing
- International Relations: Countries choosing between peaceful cooperation or hostile actions
- Social Behavior: Individuals in communities deciding whether to cooperate with others for mutual benefit or act selfishly
By studying the dynamics of the Repeated Prisoner's Dilemma, we can analyze and predict behaviors in these scenarios, as well as design systems and policies that promote cooperative behavior.
Strategy Analysis
Different strategies in the Repeated Prisoner's Dilemma can significantly influence the outcomes of interactions. By studying these strategies, we gain insights into:
- Stability of Cooperation: What conditions foster long-term cooperative behavior?
- Impact of Defection: How does a single act of defection affect future interactions?
- Adaptability and Evolution: How do strategies evolve over time in response to the actions of others?
Implemented Strategies
This project implements over 20 different strategies, each with unique characteristics and decision-making processes:
| Strategy | Description |
|---|---|
| Always Cooperate | Cooperates unconditionally. |
| Always Defect | Defects unconditionally. |
| Random | Chooses probabilistically. |
| Tit for Tat | Cooperates on the first round and imitates its opponent's previous move thereafter. |
| Friedmann | Cooperates until its opponent has defected once, and then defects for the rest of the game. |
| Joss | Plays like TFT but defects every 10% of the time. |
| Graaskamp | Plays like TFT but defects in the 50th round. |
| Probability p Cooperator | Cooperates with a probability p (example p=0.5). |
| Suspicious Tit for Tat | Defects on the first round and imitates its opponent's previous move thereafter. |
| Generous Tit for Tat | Plays like TFT but occasionally forgives defections. |
| Gradual Tit for Tat | Increases cooperation slowly after defections. |
| Imperfect Tit for Tat | Imitates opponent's last move with some probability of error. |
| Tit for Two Tats | Defects only after two consecutive defections by the opponent. |
| Two Tits for Tat | Defects twice after a single defection by the opponent. |
| Omega Tit for Tat | More complex version of TFT with additional rules. |
| Grim Trigger | Cooperates until the opponent defects once, then defects forever. |
| Backstabber | Cooperates for the first few rounds, then defects. |
| Random Backstabber | Cooperates for a random number of rounds, then defects. |
| Periodic Defector | Defects at regular intervals. |
| Vindictive | Cooperates until the opponent defects once, then defects forever. |
| Bullying | Defects initially, then cooperates if the opponent never defects. |
Tournament Design
In this comprehensive tournament, various strategies for the Repeated Prisoner's Dilemma compete against each other to evaluate their relative strengths and effectiveness. Each strategy is pitted against every other strategy to determine how well it performs across a range of scenarios. The results are recorded and analyzed to identify which strategies tend to achieve better outcomes and which may be less effective.
By conducting this tournament, we gain valuable insights into how different strategies perform in the long run and which approaches prove to be particularly robust or vulnerable to certain tactics. These insights can then be applied in real-world scenarios where strategic decision-making is crucial.
Outcomes
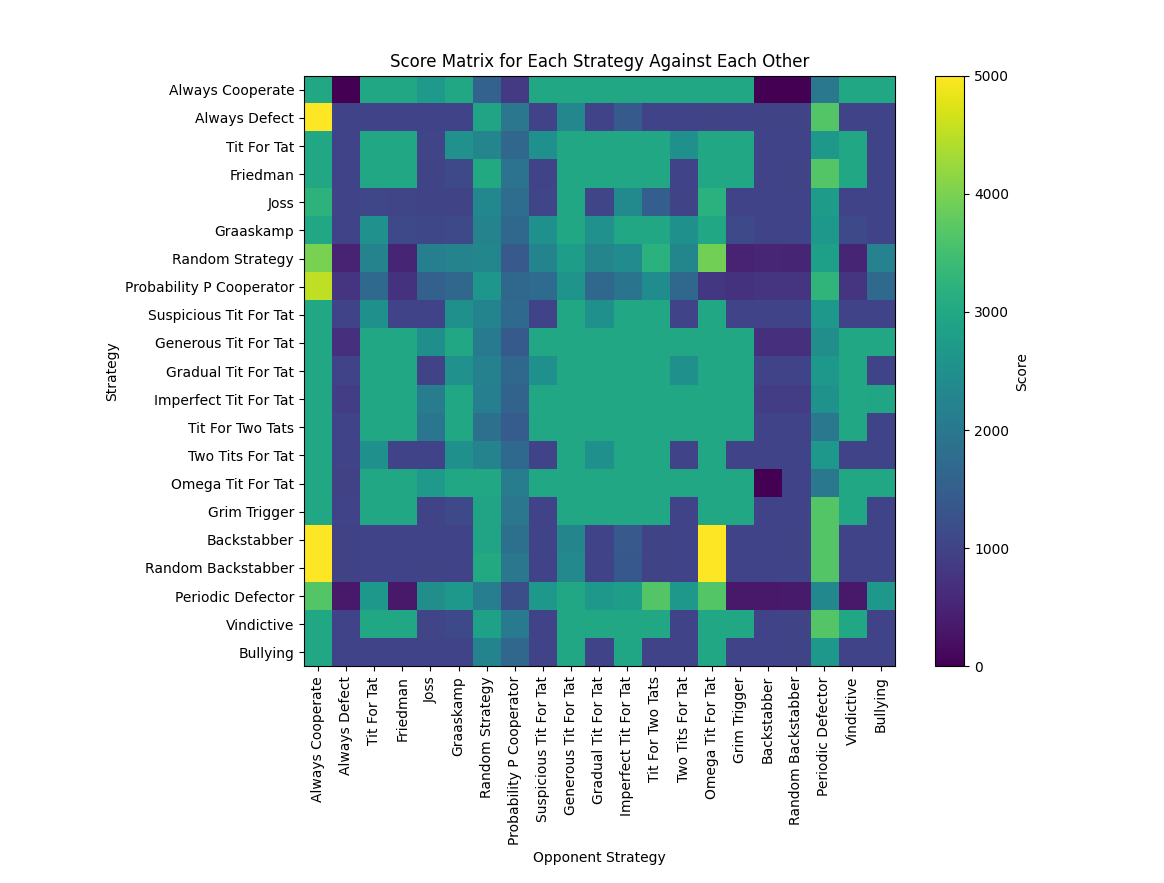
Leaderboard
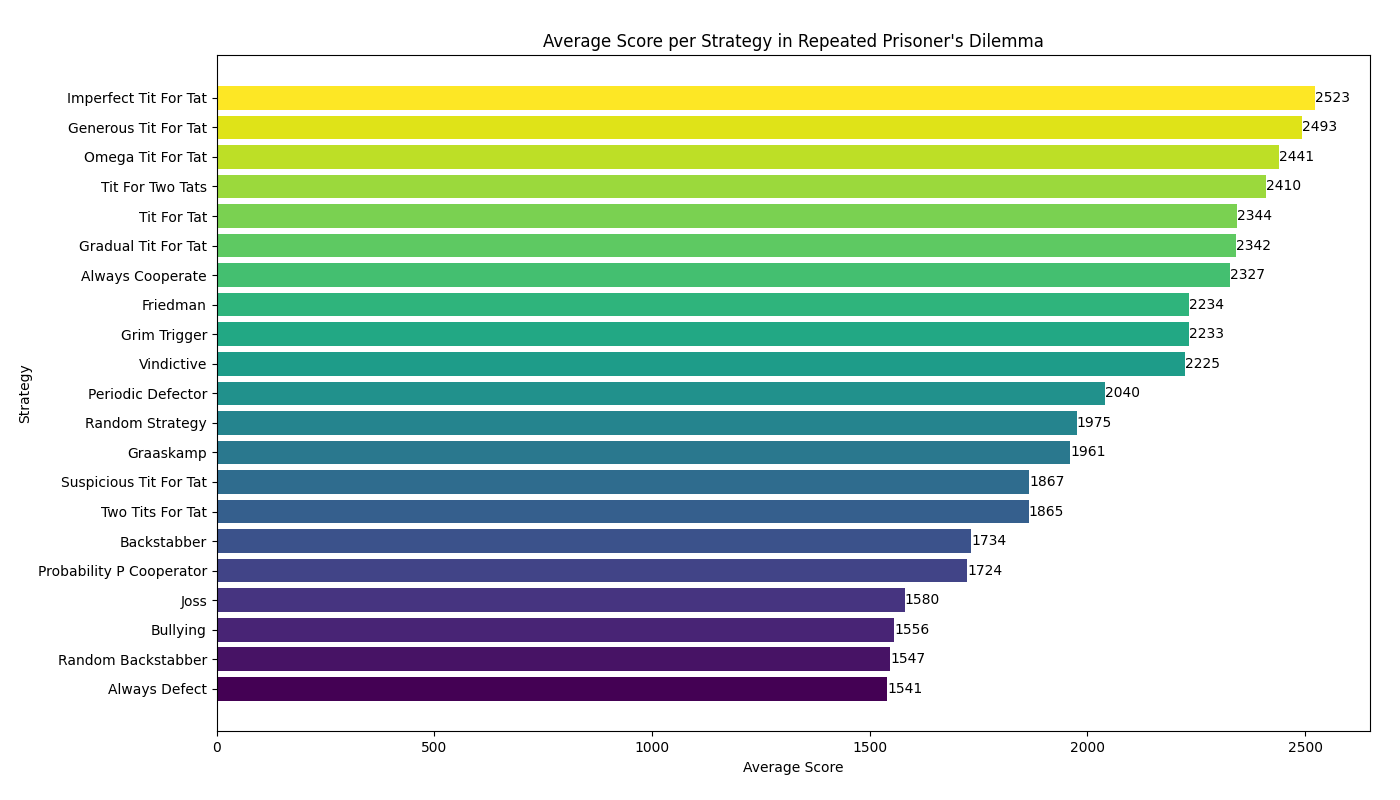
Results and Analysis
The tournament results reveal fascinating patterns about cooperation and competition. The score matrix shows how each strategy performs against every other strategy, providing a detailed view of strategic interactions and their outcomes.
The leaderboard analysis demonstrates that successful strategies typically share common characteristics: they start with cooperation (being "nice"), they respond to defection but don't hold grudges indefinitely (being "forgiving"), and they retaliate against persistent defectors (not being a "pushover").
Key Findings
"Be nice, be forgiving, but don't be a pushover."
This principle, derived from our tournament analysis, encapsulates the most successful approach to the Repeated Prisoner's Dilemma. Strategies that embody these characteristics consistently outperform purely aggressive or purely passive approaches.
Implications for Real-World Scenarios
The insights from this project have significant implications for understanding cooperation and competition in various domains:
- Business Strategy: Companies benefit from initial cooperation while maintaining the ability to respond to competitive threats
- Diplomatic Relations: Nations that start with peaceful intentions but can defend themselves tend to achieve better long-term outcomes
- Social Interactions: Individuals who are initially trusting but can appropriately respond to betrayal build stronger relationships
Future Work
Future extensions of this project could include:
- Implementing evolutionary algorithms to develop new strategies
- Adding noise and uncertainty to simulate real-world conditions
- Exploring multi-player variations of the game
- Analyzing the impact of different payoff matrices
- Studying how strategies adapt when the game length is unknown